알고리즘이란?
주어진 문제 해결 및 문제 해결에 필요한 절차와 방법을 알고리즘이라고 합니다.
여기서 절차란 어떠한 문제 해결을 위해 정해진 일련의 절차이며 계산 실행을 위한 단계적 절차를 의미하기도 합니다.
즉, 문제 풀이에 필요한 계산절차 또는 처리과정의 순서를 뜻하는 단어입니다.
효율적인 알고리즘을 선택하기 위해선 먼저 자료구조에 대한 이해가 필요합니다.
자료구조
자료구조는 데이터 사이의 논리적 관계를 표현, 조직화하는 방법입니다.
좋은 프로그램을 위해서는 적절한 자료구조와 적절한 알고리즘이 필요합니다.
기본적인 자료구조는 선형(linear)자료구조와 비선형(non-linear) 자료구조로 나뉘게 됩니다.
선형 자료구조는 이름 그대로 선, 즉 한 줄로 나열할 수 있는 자료구조입니다.
반대로 비선형은 한 줄로 나열할 수 없는 자료구조를 말합니다.
- 선형자료구조
- 배열
- 연결리스트
- 스택
- 큐
- 비선형 자료구조
- 트리
- 그래프
그럼 각각의 자료구조들에 대해 더 알아보겠습니다.
선형자료구조
배열(array)
배열은 같은 자료형을 갖는 데이터들의 집합입니다.
배열의 특징은 논리적 순서와 물리적 순서가 같다는 것입니다.

위와 같이 Integer 하나의 크기가 b라고 가정했을 때 논리적 순서와 물리적 순서가 같기 때문에 (인덱스, 값) 쌍의 집합이라고 생각할 수 있습니다.
따라서 데이터에 접근 시 순차적 접근이 아니라 인덱스를 이용해 바로 접근이 가능합니다
삽입 삭제로 인해 원소(자료) 들의 위치 이동이 발생하기 때문에 잦은 삽입, 삭제가 일어나는 경우에는 비효율적입니다.
이러한 문제 보완을 위해 연결리스트가 등장합니다.
연결리스트(linked list)
노드라는 저장 구조를 연결하여 선형 리스트를 구현하였습니다.
노드에는 하나 이상의 데이터필드와 하나 이상의 링크 필드가 존재합니다.
링크드 리스트는 배열과는 달리 논리적 순서와 물리적 순서가 일치하지 않습니다.

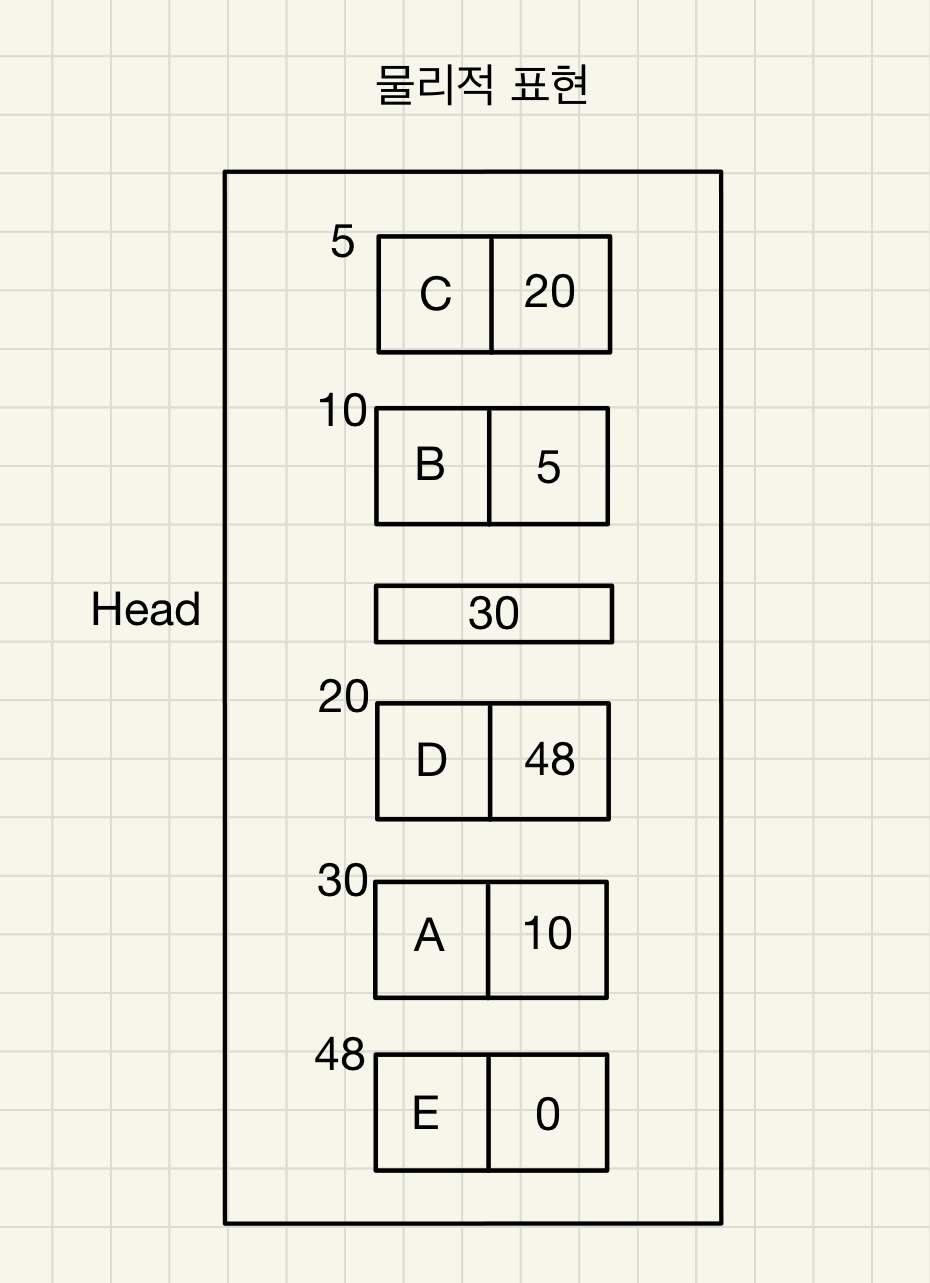
링크필드를 이용해 순서를 유지시켜주고 데이터에 접근하기 위해서는 헤드부터 링크 주소를 통해 차례로 이동하는 순차 접근이 필요합니다.
따라서 데이터가 많으면 검색이 느리다는 단점이 있습니다.
하지만 삽입, 삭제 연산은 링크 필드 조정을 통해 배열에 비해 간단하게 수행할 수 있습니다.
모든 자료구조의 구현은 앞서 말한 배열 혹 연결리스트를 이용해 구연하게 됩니다.
스택(stack)
데이터의 삽입과 삭제가 한쪽 끝에서만 수행되는 선형 리스트입니다.
후입선출(Last In First Out, LIFO)의 특징을 가집니다.

가장 위를 top 으로 표시합니다.
데이터를 밀어넣는 push, 빼는 pop 연산을 수행합니다.
스택
양쪽 끝에서 데이터 삽입과 삭제가 수행됩니다.
한쪽 끝에서는 데이터의 삽입만, 반대쪽에서는 삭제만 수행되는 선형 리스트로 선입선출(First In First Out, FIFO)의 특징을 가집니다.

삽입은 Rear 혹은 Tail에서, 삭제는 Front 혹은 Head에서 이루어집니다.
비선형자료구조
트리
노드와 노드를 연결하는 간선이 존재하는 비선형 자료구조입니다.
노드라는 정보 항목이 간선으로 연결되어 계층적인 구조를 표현합니다.
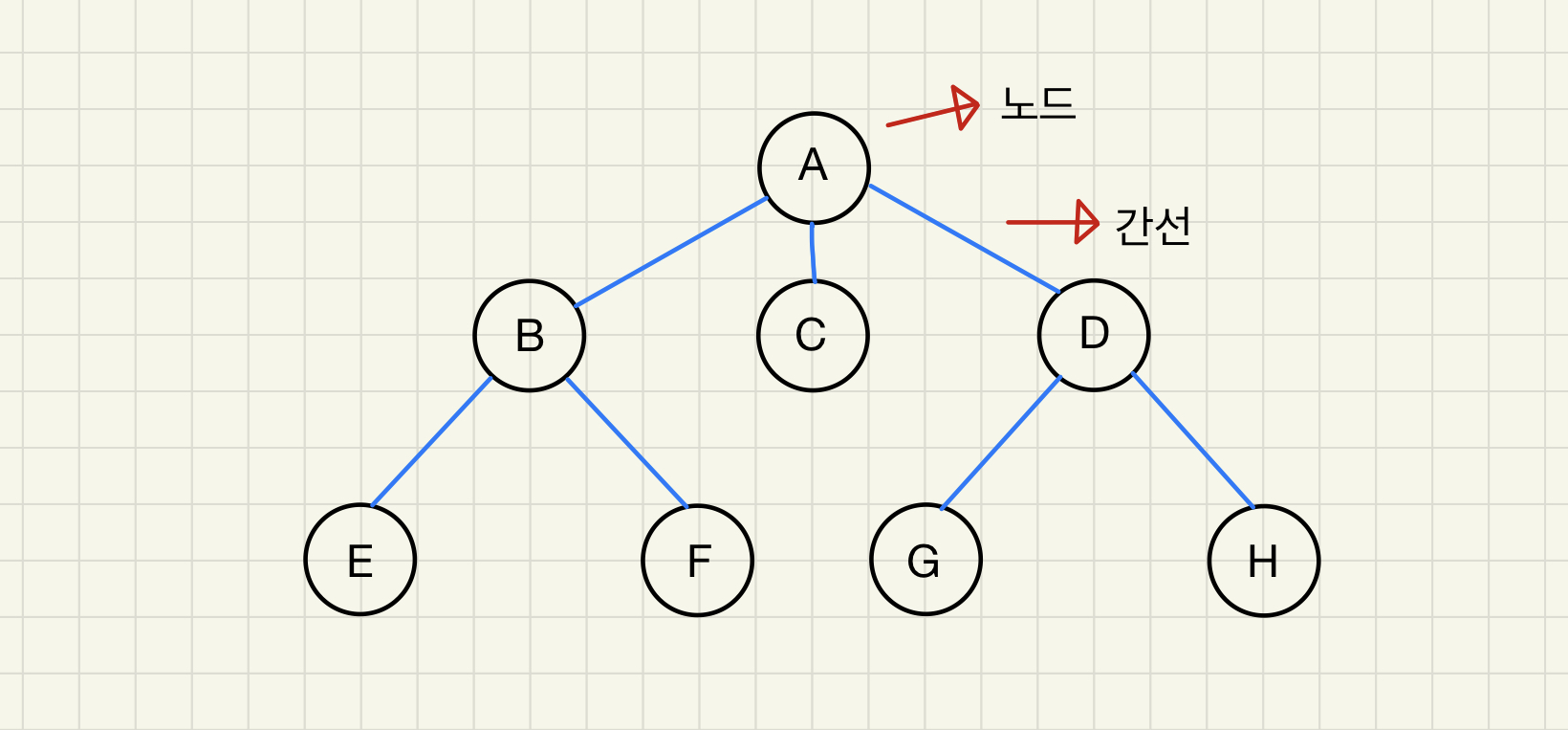
위 그림은 트리를 표현한 그림입니다.
트리는 원소 가운데 단 하나의 루트 노드가 존재합니다.
그림에서 A 노드가 루트노드입니다.
루트노드를 제외한 나머지 노드는 부분집합으로 묶여 서브트리가 됩니다.
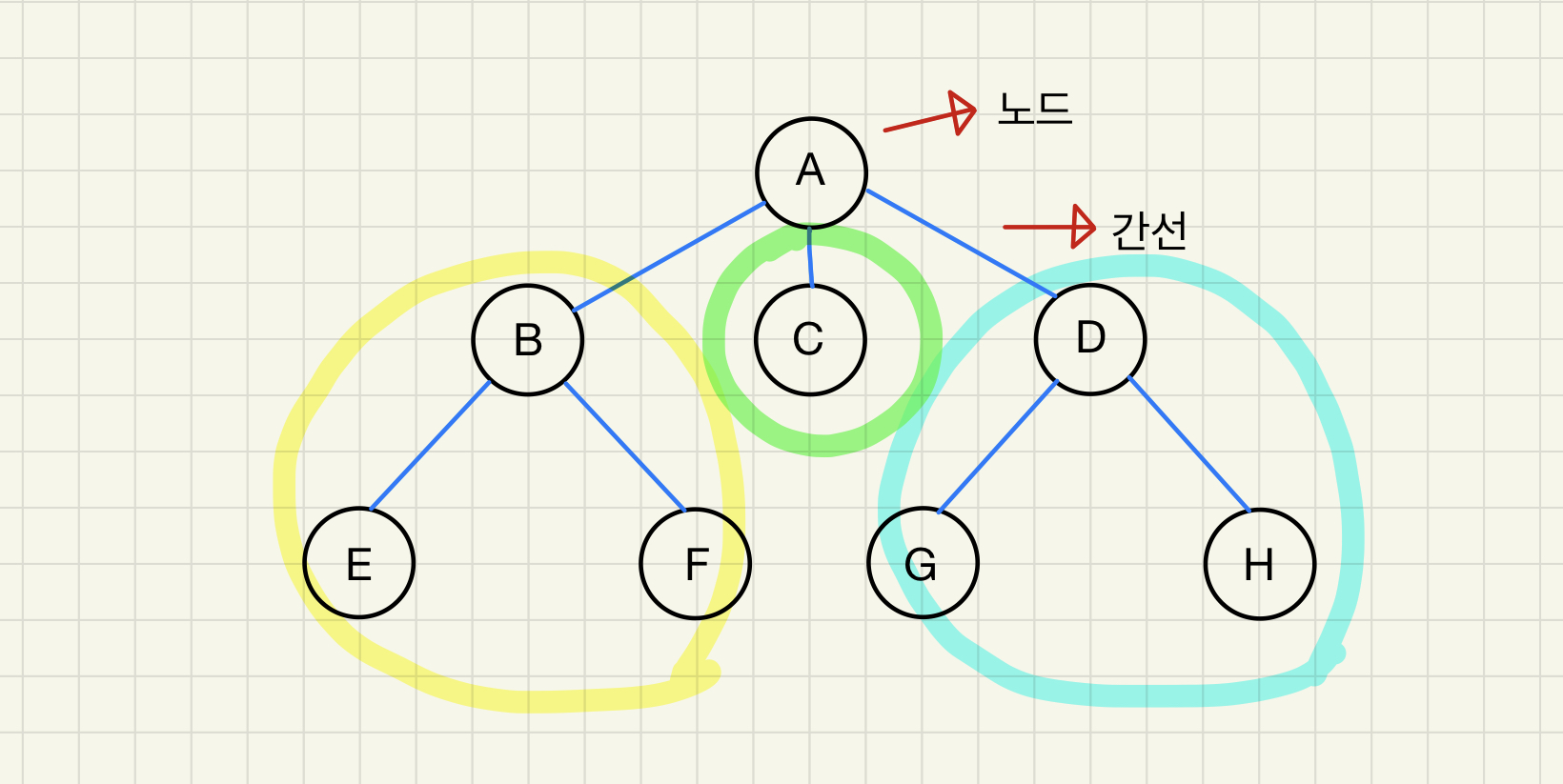
서브트리에도 루트 노드는 존재합니다.
위 그림에서는 B, C, D 가 서브트리의 루트 로드가 되겠네요.
트리에는 다양한 용어가 존재하는데요.
하나씩 알아보겠습니다.
차수(degree)
한 노드가 가진 간선의 수. 연결된 노드의
ex) A = 3, B=2, C=0
리프노드(leaf node) / 단말노드(terminal node)
차수가 0인 노드
ex) E, F, C, G, H
비단말노드
리프노드가 아닌 모든 노드
ex) A, B, D
자식노드
각 서브트리의 루트노드
ex) A 의 자식노드 = B, C, D
부모노드
자식노드의 바로 상단 노드
ex) E의 부모노드 = B
형제노드
부모가 같은 노드
ex) G, H
노드의 레벨
루트 노드로부터의 거리. 루트는 0으로 시작함
ex) A노드의 레벨 = 0, B노드의 레벨 =1
트리의 높이(깊이)
트리의 최대 레벨. 그 트리에서 가장 마지막레벨 +1
ex) 마지막 레벨(2) + 1 = 3
숲
루트노드를 잘랐을 때 생기는 집합
ex) 루트노드 A를 잘랐을 때 생기는 서브트리 3개를 숲이라고 함
그래프
그래프는 연결되어 있는 원소 간의 관계를 도형으로 표현한 자료구조로 정점과 간선의 집합으로 구성됩니다.
영어로 표현하면 Graph =(Vertext,Edge), 줄여서 G=(V, E)로 정의합니다.
그래프는 간선의 방향성 유무에 따라 방향 그래프와 무방향 그래프로 나누어집니다.

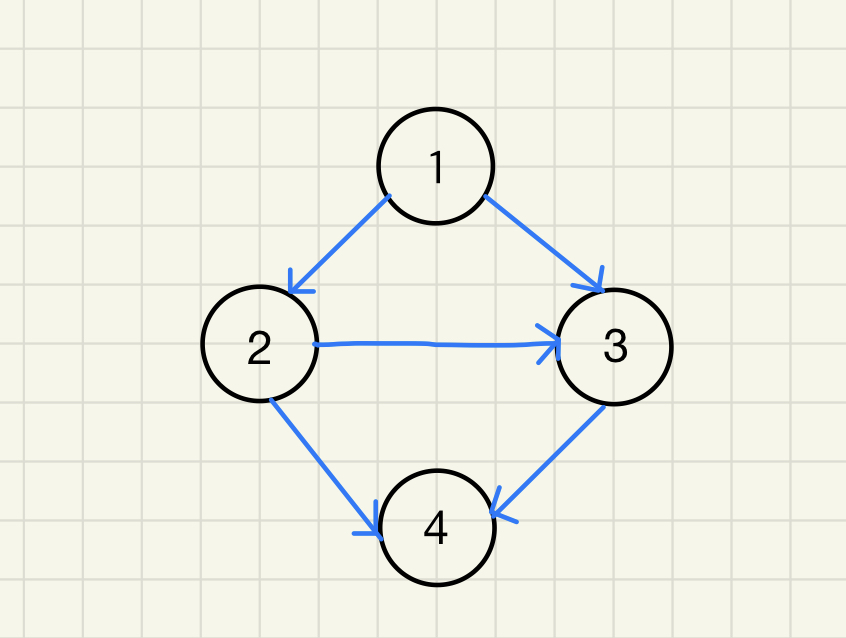
사진상에서 가장 오른쪽이 방향 그래프가 되겠네요.
두 정점이 연결되어 있다면 그 두 정점을 인접한다고 합니다.
또 둘을 잇는 간선은 부속되어있다고 표현합니다.
그래프에도 다양한 용어가 존재합니다.
차수
해당 정점에 연결된 간선의 개수
경로의 길이
경로에 존재하는 간선의 개수
깊이(높이)
트리에 속하는 노두 중에서 가장 큰 레벨에 1을 더한 것
앞서 말한 트리는 연결된 무사이클 무방향 그래프라고 생각할 수 있습니다.